How to Find the Sharpest Aperture
Thankfully, selecting the sharpest aperture is all very easy.
You’ll often see lens test reports on photo gear review sites or in photography magazines. In such tests, a chart is photographed at a succession of different apertures. Graphs of lens sharpness vs aperture are presented, and conclusions are reached on which aperture results in the sharpest image. There is nothing technically wrong with all that. Some people argue, however, that such results are only relevant if you plan to shoot a two dimensional object (such as a lens test chart) placed perpendicular to the lens axis. Well, that’s perhaps a little unfair, and not quite right. Here’s a better way to look at it: The conclusions of such tests are relevant if you intend to shoot with little regard to depth of field, i.e. if you want the subject (or at least the bit of it that’s at the focus distance) to be ultra-sharp but couldn’t care less how much depth of field you have.
Certainly, that’s not the sort of photography that we do very often. I, for example, will make deliberate decisions to go after very little depth of field (in which case I’ll choose an aperture that’s much wider than the lens’ sharpest aperture), or to go after a hell of a lot of depth of field (in which case my choice of aperture is determined by the method I set out below, and I therefore usually end up stopping down beyond the lens-test “sharpest” aperture). Some photographers like to place the limits of depth of field quite precisely (as far as that goes), and will thus base their choice of aperture on careful use of a depth of field calculator. But if, for whatever reasons, depth of field means nothing to you, and sharpness at the focus distance means an awful lot to you, then you’re best off shooting at the aperture that the lens tests tell you is the sharpest aperture. And it’s simple enough to do your own tests. No need to invest in a test chart—just shoot a flat target at a range of apertures and use your eyes to judge which aperture (or, more likely, range of apertures) results in the sharpest image. Easy.
In photographing scenes such as those shown above, there are only two things that prevent a lens from producing perfectly sharp images: optical aberrations (which are particularly bad at small f-numbers) and diffraction (which gets worse as f-number is made larger). If there were no aberrations, the sharpest aperture would be the widest one, where diffraction is at a minimum. But all lenses suffer from aberrations, so we need to stop down by several stops to get to the sharpest aperture (where aberrations have been reduced significantly, but diffraction is not yet too great). Finding that sharpest aperture is what lens test charts are for.
Chances are that your lens will at its sharpest somewhere near the middle of the aperture range. Say, f/8 or so. This is convenient. Shooting at that aperture, or thereabouts, will give you substantial depth of field, even through you may not necessarily be after it. This helps alleviate small errors in setting focus, so you almost can’t go wrong.
We’ll go on, though, to look in detail at a different situation: We’re interested in photographing a 3-dimensional scene that extends from quite near the camera to quite far. And we’re after the sharpest possible image of the entire scene, not just the bit at the focus distance. In other words, the part of the scene that’s closest to the camera, and the part that’s furthest from the camera, are just as important to us as the bit that’s at the focus distance.
Let’s take a practical example. We are shooting an architectural interior. We are using a 28 mm lens. The space we are photographing (at least that of it which appears in the frame) extends from 2 m to 14 m away from the camera. What aperture will give us the sharpest possible image? Before we go any further, you’ll probably point out that image sharpness will vary across the subject matter—the bits closest and furthest from the camera will not be as sharp as the bit that’s at the focus distance. So when we say we want the sharpest possible image, what do we mean? Well, remember what we said: The closest and furthest bits are just as important to us as the bit that’s at the focus distance. So, if we accept that an image is only as sharp as it’s least sharp part, the sensible thing to do is to find the aperture that results in those nearest and furthest bits being as sharp as possible.
In our example, the sharpest aperture will not necessarily be the same as the one found through the photographing of test charts. Things have become more complicated here. In photographing a scene with depth, we need to add the effects of defocus into the mix (defocus refers to the blurring caused by the fact that an object is not at the focus distance). We know, from basic depth of field theory, that defocus blur is reduced if we make the f-number larger. So this effect will tend to push the “sharpest” aperture further up the aperture scale. But not too far, though, because, at that end of the scale, diffraction gets really nasty. There is, however, some good that comes from this: Since we won’t be dealing with wide apertures, we can thankfully dispense with any concerns regarding aberrations, and simply perform the necessary calculations to find the aperture that results in the smallest image blur. No test charts to bother with—just sensible, valid mathematical calculations.
OK, so how do we find that ideal aperture? And while we’re at it, we had better find out what distance we should focus on.
In fact, finding the focus distance is the first step. And it’s easy. See that nice distance scale that wraps around your lens? Locate the 2 m mark and the 14 m mark. The focus distance is half-way between those marks, which works out to be 3.5 m. (You don’t have a distance scale? Don’t worry—we’ll show you a better way to do things shortly.)
Now for the aperture. Yes, we could use that depth of field scale on the lens to work out what aperture to use: Set focus distance to 3.5 m, then read the aperture that lines up with the 2 m mark (or the one that lines up with the 14 m mark—they’ll be the same).
But, no, we’re not going to do that. Why? Because the lens manufacturer who put it together did not take the effects of diffraction into account when constructing it. Don’t worry, I’m not claiming that the manufacturer is stupid, or that I know more than the likes of Nikon, Canon, etc. All those guys know all about diffraction. It’s just that there were sound historical reasons for doing what they originally did (we’re talking nearly 100 years ago), and there are now sound marketing reasons for not changing things. We’re stuck with a flawed depth of field methodology.
Let’s see what really goes on. We’ll begin by setting aperture to f/5.6. Here’s a graph that shows how image blur varies with subject distance. In this graph, we don’t ignore diffraction, so image blur is due to the combined effects of defocus and diffraction.
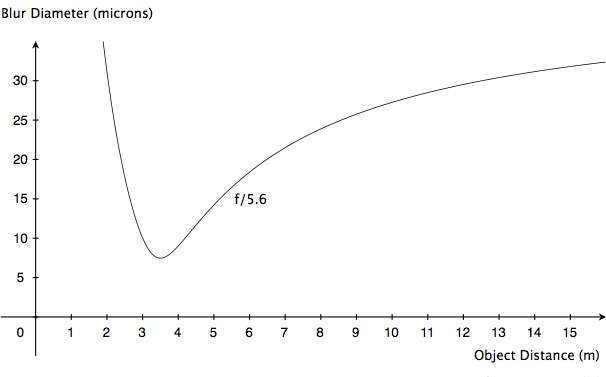
Notice that the image is sharpest for objects at the focus distance, 3.5 m, but it’s not perfectly sharp. Even at f/5.6, diffraction is adding it’s effects.
Remember what we’re after: We want those parts of the scene that are at 2 m and 14 m to be as sharp as possible. Let’s mark those distances on the graph, and let’s mark how much image blur we have at those distances:

That’s a lot of blur—well over 30 microns. Let’s see if we can do better than that. We’ll set the aperture to f/8 and see what happens:
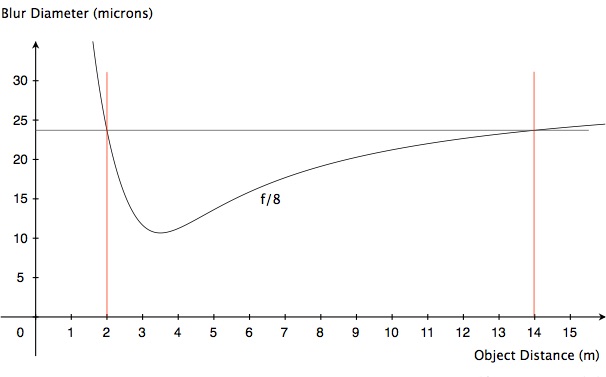
This is good. Yes, we do have more blur at the focus distance, but blur at the distance extremes is reduced to 24 or so microns.
By the way, notice what we get every time? The blur for objects at 2 m is the same as the blur for objects at 14 m. This is deliberate. We have decided that objects at at our distance extremes are equally important and that we want them to be equally sharp. We achieve that through appropriate choice of focus distance (that’s why we chose 3.5 m).
Let’s see see what happens if we go to f/11:
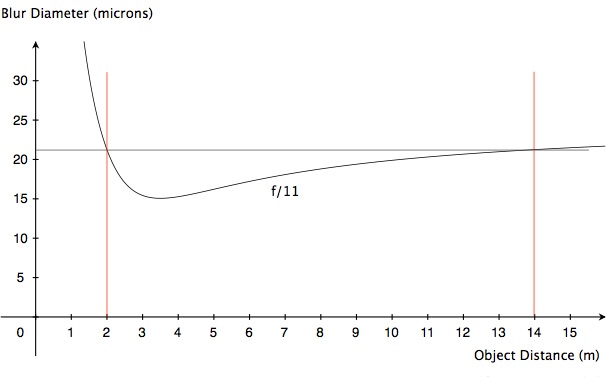
We’re onto a good thing here. Image blur for objects at the distance extremes has dropped to about 21 or so microns. Yes, we have more blur (due entirely to diffraction) at the focus distance, be we don’t care.
Well, if f/11 is good, why not go to f/16? If we do, here’s what we get:
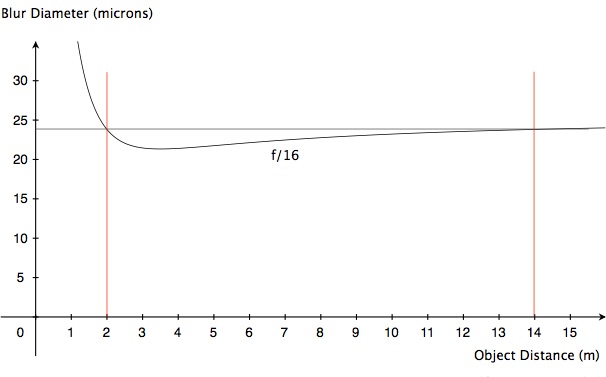
Hmmm... what’s going on here? Image blur at the distance extremes (and, indeed, everywhere else) has gone up! It’s now back to about 24 microns. Yes, as classical depth of field theory tells us, defocus blur has been reduced, but that reduction has been overwhelmed by the increase in diffraction. By increasing the f-number from f/11 to f/16, we have made things worse. Just to show what direction we’re going in, let’s have at look at the graph for f/22:
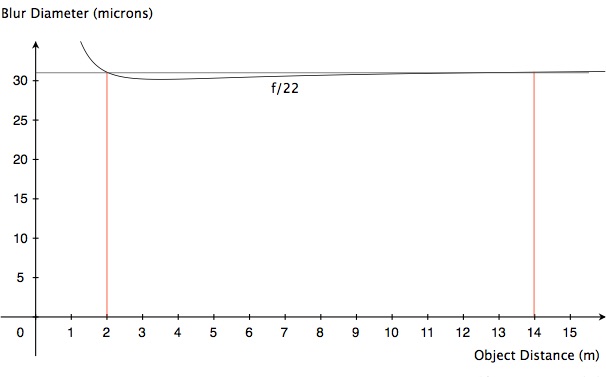
Not pretty, is it?
Clearly, f/11 is the sharpest aperture for our purposes. And we can’t do better than a blur of 21 microns for our distance extremes. That’s just physics—we’re stuck with it.
And notice something else? Going one stop above or below the ideal aperture does not cause a huge reduction in sharpness. Go two stops above or below, and it’s a whole different story.
OK, this has all been very interesting. But what’s needed is a nice, easy way to find that optimum aperture (and the optimum focus distance, too, of course). This is what we do:
We use the OptimumCS-Pro app. Here is not the place to go into the optical science behind the app—that stuff can be found elsewhere (if you’re interested). I will, however, emphasise how easy it is to use: Just set the focal length to 28 mm, move the sliders to set the near and far distances to 2 m and 14 m respectively and... that’s it, you’re done! Just read off the ideal focus distance and aperture: 3.5 m and f/11.
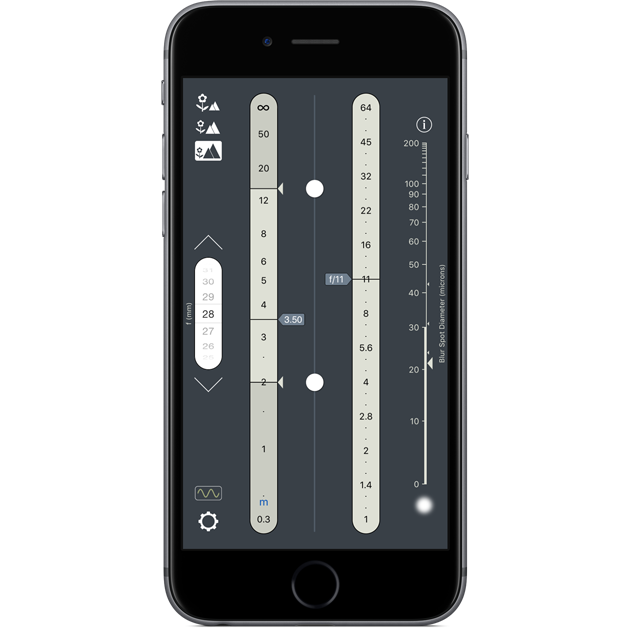
See, I wasn’t kidding when I said that selecting the sharpest aperture is easy.
And it gets even better. See that scale on the right? The large, triangular marker indicates the blur diameter for objects at the distance extremes if we shoot at the optimum aperture (we’ll have 21 microns of blur if we shoot at f/11, as we saw in the graph). The small marker just above the large one indicates how much blur we’ll end up with if we shoot at +/- 1 f-stop from the ideal aperture. And the other markers show what happens if we shoot at +/- 2 or +/- 3 f-stops from the ideal aperture. Why might you need to know this sort of thing? Well, you might have compelling reasons to shoot at other than the ideal aperture (say, in situations where you might prefer the faster shutter speed that a wider aperture gives you). In that case, you’ll know exactly what effect your decisions will have.
We’ve discussed in detail one particular example here, but the principles we’ve applied work in all cases—simply set your focal length and the distances to the nearest and furthest objects in your scene, and you’ll instantly know what focus distance and aperture to use in order to obtain the sharpest possible image.
If you use OptimumCS-Pro for a while, you’ll find that, in almost all practical situations for which the app is designed (essentially landscape and architectural photography), the optimum aperture ends up being somewhere in the mid to upper part of the aperture scale, but not usually at the very top end, and certainly nowhere near the bottom end, where aberrations are a nuisance. Isn’t that good?
In summary: If you’re shooting without regard to depth of field, you’ll shoot at the aperture that you identify, through photographing lens test charts, as the lens’ sharpest (and you’ll end up with a decent amount of depth of field anyway). If depth of field does matter to you, you’ll find the sharpest aperture for your particular composition by using OptimumCS-Pro.
© 2013-2016 George Douvos
.